|
JIPAM
| A Weighted Analytic Center for Linear Matrix Inequalities |
|
|
|
|
| |
| |
Authors: |
Irwin S. Pressman, Shafiu Jibrin, |
|
| |
Keywords:
|
Weighted analytic center, Semidefinite Programming, Linear Matrix Inequalities, Convexity, Real Algebraic Variety. |
|
| |
Date Received:
|
21/03/01 |
|
| |
Date Accepted:
|
21/03/01 |
|
| |
Subject Codes: |
90C25,49Q99,46C05,14P25
|
|
| |
Editors: |
Jonathan Borwein, |
|
| |
|
|
|
|
| |
Abstract: |
Let 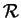 be the convex subset of be the convex subset of 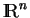 defined by defined by 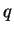 simultaneous linear matrix inequalities (LMI) simultaneous linear matrix inequalities (LMI)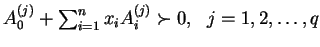 . Given a strictly positive vector . Given a strictly positive vector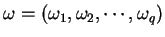 , the weighted analytic center , the weighted analytic center 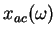 is the minimizerargmin is the minimizerargmin 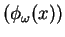 of the strictly convex function of the strictly convex function ![$phi_{omega}(x)=sum_{j=1}^{q}omega_{j}logdet[A^{(j)}(x)]^{-1$](images/023_01_JIPAM/img8.gif) over over 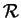 . We give a necessary and sufficient condition for a point of . We give a necessary and sufficient condition for a point of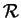 to be a weighted analytic center. We study the argmin function in this instance and show that it is a continuously differentiable open function. to be a weighted analytic center. We study the argmin function in this instance and show that it is a continuously differentiable open function.
In the special case of linear constraints, all interior points are weighted analytic centers. We show that the region 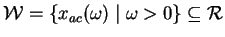 of weighted analytic centers for LMI's is not convex and does not generally equal of weighted analytic centers for LMI's is not convex and does not generally equal 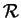 . These results imply that the techniques in linear programming of following paths of analytic centers may require special consideration when extended to semidefinite programming. We show that the region . These results imply that the techniques in linear programming of following paths of analytic centers may require special consideration when extended to semidefinite programming. We show that the region  and its boundary are described by real algebraic varieties, and provide slices of a non-trivial real algebraic variety to show that and its boundary are described by real algebraic varieties, and provide slices of a non-trivial real algebraic variety to show that  isn't convex. Stiemke's Theorem of the alternative provides a practical test of whether a point is in isn't convex. Stiemke's Theorem of the alternative provides a practical test of whether a point is in  . Weighted analytic centers are used to improve the location of standing points for the Stand and Hit method of identifying necessary LMI constraints in semidefinite programming.; . Weighted analytic centers are used to improve the location of standing points for the Stand and Hit method of identifying necessary LMI constraints in semidefinite programming.;
|
This article was printed from JIPAM
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=145
|