| |
|
|
| |
Volume 3, Issue 1, Article 15 |
|
|
|
|
|
| |
An Integral Inequality Bounding the Autocorrelation of a Pulse or Sequence at a Known Lag
|
| |
|
Authors: |
Robin Willink, |
|
| |
|
Keywords:
|
Inequalities, Auto-correlation, Bounds. |
|
| |
|
Date Received:
|
17/07/01 |
|
| |
|
Date Accepted:
|
05/11/01 |
|
| |
|
Subject Codes: |
26D15,26D07.
|
|
| |
|
Editors: |
Pietro Cerone, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
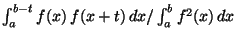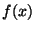This paper gives best bounds for the ratio  for any square-summable real function  on the interval ![$ (a,b]$](images/057_01_JIPAM/img3.gif) . Similarly, bounds are established for the autocorrelation of any pulse or finite-length sequence at any known lag, and the family of pulses and sequences attaining these bounds is identified. The form of this family is related to a half-cycle of a sinusoid. Stronger bounds are suggested for pulses known to be non-negative and unimodal or concave.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
Home
