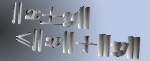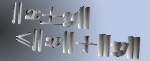| |
|
|
| |
Volume 3, Issue 5, Article 74 |
|
|
|
|
|
| |
A Hölder-type Inequality for Positive Functionals on $f$-Algebras
|
| |
|
Authors: |
Karim Boulabiar, |
|
| |
|
Keywords:
|
Hölder inequality, Positive linear functional, $f$-algebra, Uniformly complete $f$-algebra. |
|
| |
|
Date Received:
|
04/02/02 |
|
| |
|
Date Accepted:
|
31/09/02 |
|
| |
|
Subject Codes: |
06F25,47B65
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
The main purpose of this paper is to establish with a constructive proof the following Hölder-type inequality: let 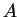 be a uniformly complete be a uniformly complete 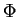 -algebra, -algebra, 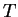 be a positive linear functional, and be a positive linear functional, and 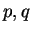 be rational numbers such that be rational numbers such that 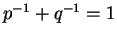 . Then the inequality . Then the inequality holds for all 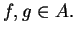
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|