| |
|
Abstract: |
Da-wei Zhang [J.M.A.A., 237 (1999):721-725] obtained the inequality between 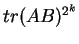 and and 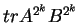 for Hermitian matrices for Hermitian matrices 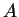 and and 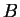 , where , where  is natural number. Here it is proved that these results hold when the power index of the product of Hermitian matrices is natural number. Here it is proved that these results hold when the power index of the product of Hermitian matrices 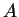 and and 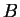 is nonnegative even number. In the meantime, it is pointed out that the relation between is nonnegative even number. In the meantime, it is pointed out that the relation between 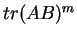 and and 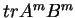 is complicated when the power index is complicated when the power index 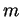 is a nonnegative odd number, therefore the above inequality can't be generalized to all nonnegative integers. As an application, we not only improve the results of Xiaojing Yang [J.M.A.A., 250 (2000), 372-374], Xinmin Yang [J.M.A.A., 263 (2001):327-333] and Fozi M. Dannan [J.Ineq. Pure and Appl. Math., 2(3) Art.34 (2001)], moreover give the complete resolution for the question of the trace inequality about the powers of Hermitian and skew Hermitian matrices that is proposed by Zhengming Jiao. is a nonnegative odd number, therefore the above inequality can't be generalized to all nonnegative integers. As an application, we not only improve the results of Xiaojing Yang [J.M.A.A., 250 (2000), 372-374], Xinmin Yang [J.M.A.A., 263 (2001):327-333] and Fozi M. Dannan [J.Ineq. Pure and Appl. Math., 2(3) Art.34 (2001)], moreover give the complete resolution for the question of the trace inequality about the powers of Hermitian and skew Hermitian matrices that is proposed by Zhengming Jiao.
|



