| |
|
|
| |
Volume 4, Issue 4, Article 68 |
|
|
|
|
|
| |
Weighted Geometric Mean Inequalities Over Cones in $R^N$
|
| |
|
Authors: |
Babita Gupta, Pankaj Jain, Lars-Erik Persson, Anna Wedestig, |
|
| |
|
Keywords:
|
Inequalities, Multidimensional inequalities, Geometric mean inequalities, Hardy type inequalities, Cones in $R^{N}$, Sharp constant. |
|
| |
|
Date Received:
|
07/11/02 |
|
| |
|
Date Accepted:
|
20/03/03 |
|
| |
|
Subject Codes: |
26D15,26D07.
|
|
| |
|
Editors: |
Bohumir Opic, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 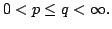 Let Let 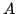 be a measurable subset of the unit sphere in be a measurable subset of the unit sphere in 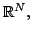 let let 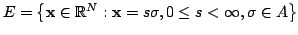 be a cone in be a cone in  and let and let 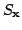 be the part of be the part of 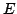 with 'radius' with 'radius'  A characterization of the weights A characterization of the weights  and and 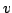 on on 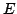 is given such that the inequality is given such that the inequality holds for all 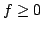 and some positive and finite constant and some positive and finite constant 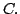 The inequality is obtained as a limiting case of a corresponding new Hardy type inequality. Also the corresponding companion inequalities are proved and the sharpness of the constant The inequality is obtained as a limiting case of a corresponding new Hardy type inequality. Also the corresponding companion inequalities are proved and the sharpness of the constant  is discussed. is discussed.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



