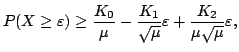JIPAM

Some Remarks on Lower Bounds of Chebyshev's Type for Half-lines  
 
  Authors: F.D. Lesley, V.I. Rotar,  
  Keywords: Inequality of Chebyshev's type.  
  Date Received: 02/10/03  
  Date Accepted: 31/10/03  
  Subject Codes:

62E20,60E05.

  
  Editors: Alexander M. Rubinov (1940-2006),  
 
  Abstract:

We prove that for any r.v. $ X$ such that $ E{X}=0, E{X^{2}}=1, $ and $ E{X^{4}}=mu $, and for any $ varepsilon geq 0$

   
$displaystyle P(Xgeq varepsilon )geq frac{K_{0}}{mu }-frac{K_{1}{sqrt{mu }} varepsilon +frac{K_{2}}{mu sqrt{mu }varepsilon ,$

where absolute constants $ K_{0}=2sqrt{3}-3approx0.464, K_{1}=1.397, $and$ K_{2}=0.0231$. The constant $ K_{0text{}}$is sharp for $ mu geq frac{3}{sqrt{3}+1}approx 1.09$. Some other bounds and examples are given.

;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=337