| |
|
|
| |
Volume 5, Issue 2, Article 38 |
|
|
|
|
|
| |
Boundary Value Problem for Second-Order Differential Operators with Mixed Nonlocal Boundary Conditions
|
| |
|
Authors: |
A. Kourta, M. Denche, |
|
| |
|
Keywords:
|
Green's Function, Non Regular Boundary Conditions, Regular Boundary Conditions, Semi group with Singularities. |
|
| |
|
Date Received:
|
15/10/2003 |
|
| |
|
Date Accepted:
|
16/04/2004 |
|
| |
|
Subject Codes: |
47E05, 35K20.
|
|
| |
|
Editors: |
Alexander G. Ramm, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper, we study a second order differential operator with mixed nonlocal boundary conditions combined weighting integral boundary condition with another two point boundary condition. Under certain conditions on the weighting functions and on the coefficients in the boundary conditions, called non regular boundary conditions, we prove that the resolvent decreases with respect to the spectral parameter in 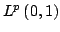 , but there is no maximal decreasing at infinity for , but there is no maximal decreasing at infinity for 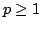 . Furthermore, the studied operator generates in . Furthermore, the studied operator generates in 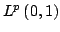 an analytic semi group with singularities for an analytic semi group with singularities for 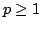 . The obtained results are then used to show the correct solvability of a mixed problem for a parabolic partial differential equation with non regular boundary conditions. . The obtained results are then used to show the correct solvability of a mixed problem for a parabolic partial differential equation with non regular boundary conditions.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



