| |
|
|
| |
Volume 5, Issue 4, Article 89 |
|
|
|
|
|
| |
New Inequalities on Polynomial Divisors
|
| |
|
Authors: |
Laurentiu Panaitopol, Doru Stefanescu, |
|
| |
|
Keywords:
|
Inequalities, Polynomials |
|
| |
|
Date Received:
|
06/05/04 |
|
| |
|
Date Accepted:
|
27/06/04 |
|
| |
|
Subject Codes: |
12D05, 12D10, 12E05, 26C05
|
|
| |
|
Editors: |
László Tóth, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this paper there are obtained new bounds for divisors of integer polynomials, deduced from an inequality on Bombieri's 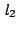 -weighted norm [1]. These bounds are given by explicit limits for the size of coefficients of a divisor of given degree. In particular such bounds are very useful for algorithms of factorization of integer polynomials. -weighted norm [1]. These bounds are given by explicit limits for the size of coefficients of a divisor of given degree. In particular such bounds are very useful for algorithms of factorization of integer polynomials.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



