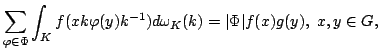JIPAM
| On Hyers-Ulam Stability of Generalized Wilson's Equation | |||||
| Authors: | Belaid Bouikhalene, | ||||
| Keywords: | Functional equations, Hyers-Ulam stability, Wilson equation, Gelfand pairs. | ||||
| Date Received: | 20/05/04 | ||||
| Date Accepted: | 15/09/04 | ||||
| Subject Codes: |
39B72. |
||||
| Editors: | Laszlo Losonczi, | ||||
| Abstract: |
In this paper, we study the Hyers-Ulam stability problem for the following functional equation
where Our results generalize and extend the Hyers-Ulam stability obtained for the Wilson's functional equation.; | ||||
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=455