JIPAM logo: Home Link
 
Home Editors Submissions Reviews Volumes RGMIA About Us
 

   
  Volume 6, Issue 2, Article 44
 
A Sawyer Duality Principle for Radially Monotone Functions in $R^n$.
    Authors: Sorina Barza, Maria Johansson, Lars-Erik Persson,  
    Keywords: Duality theorems, Radially monotone functions, Weighted inequalities.  
    Date Received: 09/02/05  
    Date Accepted: 14/02/05  
    Subject Codes:

Prim. 26D15, 47B38; Sec. 26B99, 46E30.

  
    Editors: Constantin P. Niculescu,  
 
    Abstract:

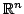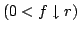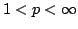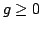Let $ f$ be a non-negative function on $ mathbb{R}^{n}$, which is radially monotone $ left( 0fdownarrow rright) $. For $ 1pinfty $, $ ggeq 0$ and $ v$ a weight function, an equivalent expression for

$displaystyle underset{fdownarrow r}{sup }frac{int_{mathbb{R}^{n}}fg}{left( int_{mathbb{R}^{n}}f^{p}vright) ^{frac{1}{p}}} $

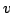is proved as a generalization of the usual Sawyer duality principle. Some applications involving boundedness of certain integral operators are also given.

         
       
  Download Screen PDF
  Download Print PDF
  Send this article to a friend
  Print this page
  

      search [advanced search] copyright 2003 terms and conditions login