JIPAM

Rate of Growth of Polynomials Not Vanishing Inside a Circle  
 
  Authors: Robert B. Gardner, Narendra K. Govil, Srinath R. Musukula,  
  Keywords: Polynomials, Restricted zeros, Growth, Inequalities.  
  Date Received: 04/01/05  
  Date Accepted: 15/04/05  
  Subject Codes:

30A10, 30C10, 30E10, 30C15.

  
  Editors: Ram N. Mohapatra,  
 
  Abstract:

A well known result due to Ankeny and Rivlin [1] states that if 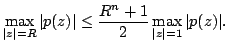$ p(z)=sum_{v=0}^n a_vz^v $ is a polynomial of degree $ n$ satisfying $ p(z)neq 0$ for $ vert zvert1$ then for $ Rgeq1$

$displaystyle max_{vert zvert=R} vert p(z)vertleq {frac{R^n+1}{2}} max_{vert zvert=1}vert p(z)vert. $

It was proposed by late Professor R.P. Boas, Jr. to obtain an inequality analogous to this inequality for polynomials having no zeros in $ vert zvertK, ;K>0 $. In this paper, we obtain some results in this direction, by considering polynomials of the form $ p(z)=a_0+sum_{v=t}^na_vz^v,; 1leq tleq n$ which have no zeros in $ vert zvertK, ;Kgeq 1$.;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=522