| |
|
|
| |
Volume 6, Issue 2, Article 53 |
|
|
|
|
|
| |
Rate of Growth of Polynomials Not Vanishing Inside a Circle
|
| |
|
Authors: |
Robert B. Gardner, Narendra K. Govil, Srinath R. Musukula, |
|
| |
|
Keywords:
|
Polynomials, Restricted zeros, Growth, Inequalities. |
|
| |
|
Date Received:
|
04/01/05 |
|
| |
|
Date Accepted:
|
15/04/05 |
|
| |
|
Subject Codes: |
30A10, 30C10, 30E10, 30C15.
|
|
| |
|
Editors: |
Ram N. Mohapatra, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
A well known result due to Ankeny and Rivlin [1] states that if 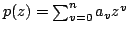 is a polynomial of degree is a polynomial of degree 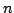 satisfying satisfying  for for 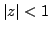 then for then for 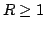 It was proposed by late Professor R.P. Boas, Jr. to obtain an inequality analogous to this inequality for polynomials having no zeros in 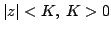 . In this paper, we obtain some results in this direction, by considering polynomials of the form . In this paper, we obtain some results in this direction, by considering polynomials of the form 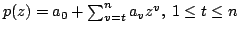 which have no zeros in which have no zeros in 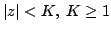 . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



