| |
|
|
| |
Volume 6, Issue 3, Article 85 |
|
|
|
|
|
| |
Outer $ \gamma$-Convex Functions on a Normed Space
|
| |
|
Authors: |
Phan Thanh An, |
|
| |
|
Keywords:
|
Convexity, Epigraph, Jensen inequality, Outer $ gamma$-convex set, Outer $ gamma$-convex function |
|
| |
|
Date Received:
|
22/03/05 |
|
| |
|
Date Accepted:
|
28/06/05 |
|
| |
|
Subject Codes: |
26A51, 26B25, 52A41.
|
|
| |
|
Editors: |
Alexander M. Rubinov (1940-2006), |
|
| |
|
|
|
|
|
| |
|
Abstract: |
For some given positive 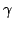 , a function , a function 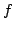 is called outer is called outer 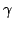 -convex if it satisfies the Jensen inequality -convex if it satisfies the Jensen inequality 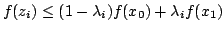 for some for some ![$ z_0colon=x_0,z_1,...,z_k colon=x_1in [x_0,x_1]$](images/087_05_JIPAM/img4.gif) satisfying satisfying  , where , where 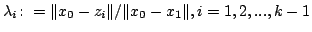 . Though the Jensen inequality is only required to hold true at some points (although the location of these points is uncertain) on the segment . Though the Jensen inequality is only required to hold true at some points (although the location of these points is uncertain) on the segment ![$ [x_0,x_1]$](images/087_05_JIPAM/img7.gif) , such a function has many interesting properties similar to those of classical convex functions. Among others it is shown that, if the infimum limit of an outer , such a function has many interesting properties similar to those of classical convex functions. Among others it is shown that, if the infimum limit of an outer 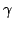 -convex function attains -convex function attains 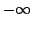 at some point then this propagates to other points, and under some assumptions, a function is outer at some point then this propagates to other points, and under some assumptions, a function is outer 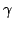 -convex iff its epigraph is an outer -convex iff its epigraph is an outer 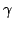 -convex set. -convex set.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



