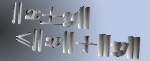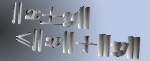| |
|
|
| |
Volume 6, Issue 3, Article 87 |
|
|
|
|
|
| |
A Minkowski-Type Inequality for the Schatten Norm
|
| |
|
Authors: |
Markus Sigg, |
|
| |
|
Keywords:
|
Schatten class, Schatten norm, Norm inequality, Minkowski inequality, Triangle inequality, Powers of operators, Schatten-Minkowski constant. |
|
| |
|
Date Received:
|
16/07/04 |
|
| |
|
Date Accepted:
|
29/06/05 |
|
| |
|
Subject Codes: |
47A30, 47B10
|
|
| |
|
Editors: |
Frank Hansen, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Let 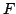 be a Schatten be a Schatten 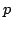 -operator and -operator and 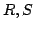 positive operators. We show that the inequality positive operators. We show that the inequality 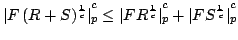 for the Schatten for the Schatten 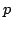 -norm -norm 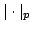 is true for is true for 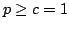 and for and for 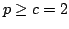 , conjecture it to be true for , conjecture it to be true for ![$ p ge c in [1,2]$](images/135_04_JIPAM/img8.gif) , give counterexamples for the other cases, and present a numerical study for , give counterexamples for the other cases, and present a numerical study for 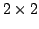 matrices. Furthermore, we have a look at a generalisation of the inequality which involves an additional factor matrices. Furthermore, we have a look at a generalisation of the inequality which involves an additional factor 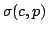 . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|