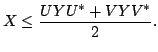JIPAM
| Hermitian Operators and Convex Functions | |||||
| Authors: | Jean-Christophe Bourin, | ||||
| Keywords: | Hermitian operators, eigenvalues, operator inequalities, Jensen's inequality. | ||||
| Date Received: | 06/04/05 | ||||
| Date Accepted: | 10/11/05 | ||||
| Subject Codes: |
47A30 47A63. |
||||
| Editors: | Frank Hansen, | ||||
| Abstract: |
We establish several convexity results for Hermitian matrices. For instance: Let
| ||||
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=615