| |
|
|
| |
Volume 6, Issue 5, Article 139 |
|
|
|
|
|
| |
Hermitian Operators and Convex Functions
|
| |
|
Authors: |
Jean-Christophe Bourin, |
|
| |
|
Keywords:
|
Hermitian operators, eigenvalues, operator inequalities, Jensen's inequality. |
|
| |
|
Date Received:
|
06/04/05 |
|
| |
|
Date Accepted:
|
10/11/05 |
|
| |
|
Subject Codes: |
47A30 47A63.
|
|
| |
|
Editors: |
Frank Hansen, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
We establish several convexity results for Hermitian matrices. For instance: Let 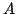 , ,  be Hermitian and let be Hermitian and let 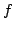 be a convex function. If be a convex function. If 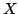 and and 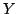 stand for stand for 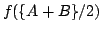 and and 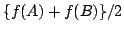 respectively, then there exist unitaries respectively, then there exist unitaries 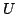 , , 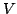 such that such that Consequently, 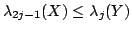 , where , where 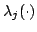 are the eigenvalues arranged in decreasing order. are the eigenvalues arranged in decreasing order.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



