| |
|
Abstract: |
The well-known second order moment Heisenberg-Weyl inequality (or uncertainty relation) in Fourier Analysis states: Assume that 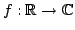 is a complex valued function of a random real variable is a complex valued function of a random real variable 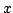 such that such that 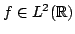 . Then the product of the second moment of the random real . Then the product of the second moment of the random real 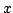 for for 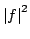 and the second moment of the random real and the second moment of the random real 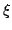 for for  is at least is at least 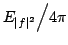 , where , where  is the Fourier transform of is the Fourier transform of  , such that , such that  , , 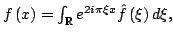 and and 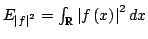 . . This uncertainty relation is well-known in classical quantum mechanics. In 2004, the author generalized the afore-mentioned result to higher order moments and in 2005, he investigated a Heisenberg-Weyl type inequality without Fourier transforms. In this paper, a sharpened form of this generalized Heisenberg-Weyl inequality is established in Fourier analysis. Afterwards, an open problem is proposed on some pertinent extremum principle.These results are useful in investigation of quantum mechanics.
|



