JIPAM
| Hyers-Ulam-Rassias Stability of the $K$-Quadratic Functional Equation | ||||
| Authors: | Mohamed Ait Sibaha, Belaid Bouikhalene, Elhoucien Elqorachi, | |||
| Keywords: | Group, Additive equation, Quadratic equation, Hyers-Ulam-Rassias stability. | |||
| Date Received: | 26/01/07 | |||
| Date Accepted: | 08/06/07 | |||
| Subject Codes: |
39B82, 39B52, 39B32. |
|||
| Editors: | Kazimierz Nikodem, | |||
| Abstract: |
In this paper we obtain the Hyers-Ulam-Rassias stability for the functional equation 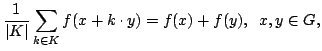 | |||
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=902