Adler, R. J., Taylor, J. E.: Random Fields and Geometry. Springer, New York (2007) MR2319516

   Aizenman, M., Molchanov, S.: Localization at large disorder and at extreme energies: an elementary derivation. Commun. Math. Phys. 157, 245–278 (1993) MR1244867

   Aizenman, M., Schenker, J. H., Friedrich, R. M., Hundertmark, D.: Finite-volume fractional-moment criteria for Anderson localization. Commun. Math. Phys. 224, 219–253 (2001) MR1868998

   Anderson, G. W., Guionnet, A., Zeitouni, O.: An introduction to random matrices. Cambridge Studies in Advanced Mathematics, vol. 118. Cambridge University Press, Cambridge (2010) MR2760897

   Anderson, P. W.: Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492–1505 (1958)

   Astrauskas, A.: On high-level exceedances of i.i.d. random fields. Stat. Probab. Letters 52, 271–277 (2001) MR1838215

   Astrauskas, A.: On high-level exceedances of Gaussian fields and the spectrum of random Hamiltonians. Acta Appl. Math. 78, 35–42 (2003) MR2021766

   Astrauskas, A.: Strong laws for exponential order statistics and spacings. Lithuanian Math. J. 46, 385–397 (2006) MR2320358

   Astrauskas, A.: Poisson-type limit theorems for eigenvalues of finite-volume Anderson Hamiltonian. Acta Appl. Math. 96, 3–15 (2007) MR2327522

   Astrauskas, A.: Extremal theory for spectrum of random discrete Schrödinger operator. I. Asymptotic expansion formulas. J. Stat. Phys. 131, 867–916 (2008) MR2398957

   Astrauskas, A.: Extremal theory for spectrum of random discrete Schrödinger operator. II. Distributions with heavy tails. J. Stat. Phys. 146, 98–117 (2012) MR2873003

   Astrauskas, A.: Extremal theory for spectrum of random discrete Schrödinger operator. III. Localization properties. J. Stat. Phys. 150, 889–907 (2013) MR3028390

   Astrauskas, A.: Asymptotic expansion formulas for the largest eigenvalues of finite-volume Anderson Hamiltonians with fractional double exponential tails. In preparation (2016)

   Astrauskas, A., Molchanov, S. A.: Limit theorems for the ground states of the Anderson model. Funkts. Anal. Prilozhen. 26:4, 92–95 (1992); English transl.: Funct. Anal. Appl. 26, 305–307 (1992) MR1209956

   Auffinger, A., Ben Arous, G., Péché, S.: Poisson convergence for the largest eigenvalues of heavy tailed random matrices. Ann. Inst. H. Poincaré Probab. Statist. 45, 589–610 (2009) MR2548495

   Bai, Z. D., Yin, Y. Q.: Necessary and sufficient conditions for almost sure convergence of the largest eigenvalue of a Wigner matrix. Ann. Probab. 16, 1729–1741 (1988) MR0958213

   Benaych-Georges, F., Péché, S.: Localization and delocalization for heavy tailed band matrices. Ann. Inst. H. Poincaré Probab. Statist. 50, 1385–1403 (2014) MR3269999

   Bingham, N. H., Goldie, C. M., Teugels, J. L.: Regular Variation. Cambridge University Press, Cambridge (1987) MR0898871

   Binswanger, K., Embrechts, P.: Longest runs in coin tossing. Insurance Math. Econom. 15, 139–149 (1994) MR1333087

   Biroli, G., Bouchaud, J.-P., Potters, M.: On the top eigenvalue of heavy-tailed random matrices. Europhys. Lett. EPL 78(1), Art 10001, 5 pp (2007) MR2371333

   Bishop, M., Wehr, J.: Ground state energy of the one-dimensional discrete random Schrödinger operator with Bernoulli potential. J. Stat. Phys. 147, 529–541 (2012) MR2923328

   Biskup, M., Fukushima, R., König, W.: Eigenvalue fluctuations for lattice Anderson Hamiltonians. Preprint arXiv:1406.5268 [math.PR] (2014) MR3537879

   Biskup, M., König, W.: Long-time tails in the parabolic Anderson model with bounded potential. Ann. Probab. 29, 636–682 (2001) MR1849173

   Biskup, M., König, W.: Eigenvalue order statistics for random Schrödinger operators with doubly-exponential tails. Commun. Math. Phys. 341, 179–218 (2016) MR3439225

   Bourgade, P., Erd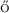s, L., Yau, H.-T.: Edge universality of beta ensembles. Commun. Math. Phys. 332, 261–353 (2014) MR3253704

   Carmona, R., Klein, A., Martinelli, F.: Anderson localization for Bernoulli and other singular potentials. Commun. Math. Phys. 108, 41–66 (1987) MR0872140

   de Haan, L., Ferreira, A.: Extreme Value Theory: An Introduction. Springer, New York (2006) MR2234156

   Deheuvels, P.: Strong laws for the kth order statistics when k ≤ clog ₂n. Probab. Theory Relat. Fields 72, 133–154 (1986) MR0835163

   Devroye, L.: Upper and lower class sequences for minimal uniform spacings. Z. Wahrsch. Verw. Gebiete 61, 237–254 (1982) MR0675613

   Elgart, A., Krüger, H., Tautenhahn, M., Veselić, I.: Discrete Schrödinger operators with random alloy-type potential. In: Benguria, R., Friedman, E., Mantoiu, M. (eds.), Spectral Analysis of Quantum Hamiltonians, Operator Theory: Advances and Applications, vol. 224, pp. 107–131. Springer, Basel (2012) MR2962857

   Embrechts, P., Kluppelberg, C., Mikosch, T.: Modelling Extremal Events for Insurance and Finance. Springer, Berlin (1997) MR1458613

   Erd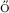s, L., Knowles, A., Yau, H.-T., Yin, J.: Spectral statistics of Erd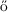s-Rényi graphs I: Local semicircle law. Ann. Probab. 41, 2279–2375 (2013a) MR3098073

   Erd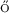s, L., Knowles, A., Yau, H.-T., Yin, J.: Delocalization and diffusion profile for random band matrices. Commun. Math. Phys. 323, 367–416 (2013b) MR3085669

   Fiodorov, A., Muirhead, S.: Complete localisation and exponential shape of the parabolic Anderson model with Weibull potential field. Electron. J. Probab. 19, no. 58, 1–27 (2014) MR3238778

   Fröhlich, J., Martinelli, F., Scoppola, E., Spencer, T.: Constructive proof of localization in the Anderson tight binding model. Commun. Math. Phys. 101, 21–46 (1985) MR0814541

   Fröhlich, J., Spencer, T.: Absence of diffusion in the Anderson tight binding model for large disorder or low energy. Commun. Math. Phys. 88, 151–184 (1983) MR0696803

   Gärtner, J., den Hollander, F.: Correlation structure of intermittency in the parabolic Anderson model. Probab. Theory Relat. Fields 114, 1–54 (1999) MR1697138

   Gärtner, J., König, W., Molchanov, S. A.: Almost sure asymptotics for the continuous parabolic Anderson model. Probab. Theory Relat. Fields 118, 547–573 (2000) MR1808375

   Gärtner, J., König, W., Molchanov, S.: Geometric characterization of intermittency in the parabolic Anderson model. Ann. Probab. 35, 439–499 (2007) MR2308585

   Gärtner, J., Molchanov, S. A.: Parabolic problems for the Anderson model. I. Intermittency and related topics. Commun. Math. Phys. 132, 613–655 (1990) MR1069840

   Gärtner, J., Molchanov, S. A.: Parabolic problems for the Anderson model. II. Second-order asymptotics and structure of high peaks. Probab. Theory Relat. Fields 111, 17–55 (1998) MR1626766

   Germinet, F., Klopp, F.: Enhanced Wegner and Minami estimates and eigenvalue statistics of random Anderson models at spectral edges. Ann. H. Poincaré 14, 1263–1285 (2013) MR3070753

   Germinet, F., Klopp, F.: Spectral statistics for random Schrödinger operators in the localized regime. J. Europ. Math. Soc. 16:9, 1967–2031 (2014) MR3273314

   Götze, F., Naumov, A., Tikhomirov, A. N.: Local semicircle law under moment conditions. Part II: Localization and delocalization. Preprint arXiv:1511.00862v2 [math.PR] (2015)

   Grenkova, L. N., Molchanov, S. A., Sudarev, Yu. N.: On the basic states of one-dimensional disordered structures. Commun. Math. Phys. 90, 101–124 (1983). MR0714614

   Grenkova, L. N., Molchanov, S. A., Sudarev, Yu. N.: The structure of the edge of the multidimensional Anderson model spectrum. Teoret. Mat. Fiz. 85:1, 32–40 (1990); English transl.: Theor. Math. Phys. 85:1, 1033–1039 (1990) MR1083950

   van der Hofstad, R., König, W., Mörters, P.: The universality classes in the parabolic Anderson model. Commun. Math. Phys. 267, 307–353 (2006) MR2249772

   van der Hofstad, R., Mörters, P., Sidorova, N.: Weak and almost sure limits for the parabolic Anderson model with heavy-tailed potential. Ann. Appl. Prob. 18, 2450-2494 (2008) MR2474543

   Hundertmark, D.: A short introduction to Anderson localization. In: Analysis and stochastics of growth processes and interface models, pp. 194–218. Oxford Univ. Press, Oxford (2008) MR2603225

   Killip, R., Nakano, F.: Eigenfunction statistics in the localized Anderson model. Ann. H. Poincaré 8, 27–36 (2007) MR2299191

   Kirsch, W.: An invitation to random Schrödinger operator. In: Random Schrödinger operators, Panor. Synthéses, vol. 25, pp. 1–119. Soc. Math. France, Paris (2008) MR2509110

   Kirsch, W., Metzger, B.: The integrated density of states for random Schrödinger operators. In: Spectral theory and mathematical physics: a Festschrift in honor of Barry Simon’s 60th birthday, Proc. Sympos. Pure Math., vol. 76, pp. 649–696. Amer. Math. Soc., Providence (2007) MR2307751

   Klopp, F.: Band edge behavior of the integrated density of states of random Jacobi matrices in dimension 1. J. Stat. Phys. 90, 927–947 (1998) MR1616938

   Klopp, F.: Precise high energy asymptotics for the integrated density of states of an unbounded random Jacobi matrix. Rev. Math. Phys. 12(4), 575–620 (2000) MR1763843

   Klopp, F.: Decorrelation estimates for the eigenlevels of the discrete Anderson model in the localized regime. Commun. Math. Phys. 303, 233–260 (2011) MR2775121

   König, W.: The Parabolic Anderson Model. Birkhäuser, Basel (2016)

   König, W., Lacoin, H., Mörters, P., Sidorova, N.: A two cities theorem for the parabolic Anderson model. Ann. Probab. 37, 347–392 (2009) MR2489168

   Lankaster, P.: Theory of Matrices. Academic Press, London (1969) MR0245579

   Leadbetter, M. R., Lindgren, G., Rootzén, H.: Extremes and Related Properties of Random Sequences and Processes. Springer, New York (1983) MR0691492

   Lee, J. O., Yin, J.: A necessary and sufficient condition for edge universality of Wigner matrices. Duke Math. J. 163(1), 117–173 (2014) MR3161313

   Mehta, M. L.: Random Matrices, 3rd ed. Elsevier/Academic Press, Amsterdam (2004) MR2129906

   Minami, N.: Local fluctuation of the spectrum of a multidimensional Anderson tight binding model. Commun. Math. Phys. 177, 709–725 (1996) MR1385082

   Minami, N.: Theory of point processes and some basic notions in energy level statistics. In: Probability and Mathematical Physics. CRM Proceedings and Lecture Notes, vol. 42, pp. 353–398. Amer. Math. Soc., Providence (2007) MR2352280

   Molchanov, S.: The local structure of the spectrum of the one-dimensional Schrödinger operator. Commun. Math. Phys. 78, 429–446 (1981) MR0603503

   Molchanov, S. A.: Lectures on random media. In: Lectures on Probability Theory, Ecole d’Eté de Probabilités de Saint-Flour XXII-1992. Lect. Notes in Math., vol. 1581, pp. 242–411. Springer, Berlin (1994) MR1307415

   Molchanov, S., Vainberg, B.: Scattering on the system of the sparse bumps: multidimensional case.Applicable Analysis 71, 167–185 (1998) MR1690097

   Molchanov, S., Vainberg, B.: Spectrum of multidimensional Schrödinger operators with sparse potentials. In: Santosa, F., Stakgold, I. (eds.) Analytical and Computational Methods in Scattering and Applied Mathematics, pp. 231–253. Chapman and Hall/CRC (2000) MR1756700

   Molchanov, S., Zhang, H.: The parabolic Anderson model with long range basic Hamiltonian and Weibull type random potential. In: Deuschel, J.-D., Gentz, B., König, W., von Renesse, M., Scheutzow, M., Schmock, U. (eds.) Probability in Complex Physical Systems, In Honour of Erwin Bolthausen and Jürgen Gärtner, Springer Proceedings in Mathematics, vol. 11, pp. 13–31. Springer, Heidelberg (2012) MR3372843

   Muirhead, S., Pymar, R.: Localization in the Bouchaud-Anderson model. Preprint arXiv: 1411.4032v2 [math.PR] (2014) MR3549713

   Pastur, L., Figotin, A.: Spectra of Random and Almost-Periodic Operators. Springer, Berlin (1992) MR1223779

   Resnick, S. I.: Extreme Values, Regular Variation, and Point Processes. Springer, Berlin (1987) MR0900810

   Shorack, G. R., Wellner, J. A.: Empirical Processes with Applications to Statistics. Wiley, New York (1986) MR0838963

   Sidorova, N., Twarowski, A.: Localisation and ageing in the parabolic Anderson model with Weibull potential. Ann. Probab. 42, 1666–1698 (2014) MR3262489

   Simon, B., Wolff, T.: Singular continuous spectra under rank one perturbations and localization for random Hamiltonians. Commun. Pure Appl. Math. 39, 75–90 (1986) MR0820340

   Sodin, S.: The spectral edge of some random band matrices. Annals of Mathematics 172, 2223–2251 (2010) MR2726110

   Soshnikov, A.: Universality at the edge of the spectrum in Wigner random matrices. Commun. Math. Phys. 207, 697–733 (1999) MR1727234

   Soshnikov, A.: Poisson statistics for the largest eigenvalues of Wigner random matrices with heavy tails. Elect. Commun. Probab. 9, 82–91 (2004) MR2081462

   Spencer, T.: Random banded and sparse matrices (Chapter 23). In: Akemann, G., Baik, J., Di Francesco, P. (eds.) Oxford Handbook on Random Matrix Theory. Oxford University Press, Oxford (2011) MR2932643

   Stolz, G.: An introduction to the mathematics of Anderson localization. Contemp. Math. 552, 71–108 (2011) MR2868042

   Sznitman, A.-S.: Brownian Motion, Obstacles and Random Media. Springer, Berlin (1998) MR1717054

   Tao, T., Vu, V.: Random matrices: Universality of local eigenvalue statistics up to the edge. Commun. Math. Phys. 298, 549–572 (2010) MR2669449

   Tao, T., Vu, V.: Random matrices: the universality phenomenon for Wigner ensembles. In: Modern aspects of random matrix theory, Proc. Sympos. Appl. Math., vol. 72, pp. 121–172. Amer. Math. Soc., Providence (2014) MR3288230

   Tautenhahn, M., Veselić, I.: Discrete alloy-type models: regularity of distributions and recent results. Markov Process. Related Fields 21, 823–846 (2015) MR3494776

   Vu, V., Wang, K.: Random weighted projections, random quadratic forms and random eigenvectors. Random Struct. Alg. 47, 792–821 (2015) MR3418916

   Wellner, J. A.: Limit theorems for the ratio of the empirical distribution function to the true distribution function. Z. Wahrsch. Verw. Gebiete 45, 73–88 (1978) MR0651392