|
|
Coagulation and diffusion: A probabilistic perspective on the Smoluchowski PDE
|
|
Alan Michael Hammond, U.C. Berkeley |
|
Full Text: PDF |
References
[1] David J. Aldous. Deterministic and stochastic models for coalescence (aggregation and coagulation): a review of the mean-field theory for probabilists. Bernoulli, 5(1):3–48, 1999. MR1673235
[2] Omer Angel, Nathanaël Berestycki, and Vlada Limic. Global divergence of spatial coalescents. Probab. Theory Related Fields, 152(3–4):625–679, 2012. MR2892958
[3] J. M. Ball and J. Carr. The discrete coagulation-fragmentation equations: existence, uniqueness, and density conservation. J. Statist. Phys., 61(1–2):203–234, 1990. MR1084278
[4] Nathanaël Berestycki. Recent progress in coalescent theory, volume 16 of Ensaios Matemáticos [Mathematical Surveys]. Sociedade Brasileira de Matemática, Rio de Janeiro, 2009. MR2574323
[5] Ludwig Boltzmann. Lectures on gas theory. Translated by Stephen G. Brush. University of California Press, Berkeley, 1964. MR0158708
[6] J. T. Cox. Coalescing random walks and voter model consensus times on the torus in Zd. Ann. Probab., 17(4):1333–1366, 1989. MR1048930
[7] László Erd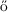 s, Benjamin Schlein, and Horng-Tzer Yau. Derivation
of the Gross-Pitaevskii equation for the dynamics of Bose-Einstein
condensate. Ann. of Math. (2), 172(1):291–370, 2010. MR2680421
s, Benjamin Schlein, and Horng-Tzer Yau. Derivation
of the Gross-Pitaevskii equation for the dynamics of Bose-Einstein
condensate. Ann. of Math. (2), 172(1):291–370, 2010. MR2680421
[8] Lawrence C. Evans. Partial differential equations, volume 19 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, 1998. MR1625845
[9] Isabelle Gallagher, Laure Saint-Raymond, and Thierry Bodineau. The Brownian motion as the limit of a deterministic system of hard-spheres. arXiv:1305.7405, 2013. MR3455156
[10] Alan Hammond and Fraydoun Rezakhanlou. Kinetic limit for a system of coagulating planar Brownian particles. J. Stat. Phys., 124(2–4):997–1040, 2006. MR2264632
[11] Alan Hammond and Fraydoun Rezakhanlou. The kinetic limit of a system of coagulating Brownian particles. Arch. Ration. Mech. Anal., 185(1):1–67, 2007. MR2308858
[12] Alan Hammond and Fraydoun Rezakhanlou. Moment bounds for the Smoluchowski equation and their consequences. Comm. Math. Phys., 276(3):645–670, 2007. MR2350433
[13] Reinhard Illner and Mario Pulvirenti. Global validity of the Boltzmann equation for a two-dimensional rare gas in vacuum. Comm. Math. Phys., 105(2):189–203, 1986. MR0849204
[14] J. F. C. Kingman. The coalescent. Stochastic Process. Appl., 13(3):235–248, 1982. MR0671034
[15] J. F. C. Kingman. On the genealogy of large populations. J. Appl. Probab., (Special Vol. 19A):27–43, 1982. Essays in statistical science. MR0633178
[16] O.E. Lanford III. Time evolution of large classical systems. Lecture Notes in Physics, 38:1–111, 1975. MR0479206
[17] Reinhard Lang and Xuan-Xanh Nguyen. Smoluchowski’s theory of coagulation in colloids holds rigorously in the Boltzmann-Grad limit. Z. Wahrsch. Verw. Gebiete, 54:227–280, 1980. MR0602510
[18] Philippe Laurençot and Stéphane Mischler. Global existence for the discrete diffusive coagulation-fragmentation equations in L1. Rev. Mat. Iberoamericana, 18(3):731–745, 2002. MR1954870
[19] J. B. McLeod. On an infinite set of non-linear differential equations. Quart. J. Math. Oxford Ser. (2), 13:119–128, 1962. MR0139822
[20] J. B. McLeod. On the scalar transport equation. Proc. London Math. Soc. (3), 14:445–458, 1964. MR0162110
[21] J. R. Norris. Smoluchowski’s coagulation equation: uniqueness, nonuniqueness and a hydrodynamic limit for the stochastic coalescent. Ann. Appl. Probab., 9(1):78–109, 1999.
[22] J. R. Norris. Cluster coagulation. Comm. Math. Phys., 209(2):407–435, 2000. MR1737990
[23] J. R. Norris. Measure solutions for the Smoluchowski coagulation-diffusion equation. arXiv:1408.5228, 2014. MR1682596
[24] Mojtaba Ranjbar and Fraydoun Rezakhanlou. Equilibrium fluctuations for a model of coagulating-fragmenting planar Brownian particles. Comm. Math. Phys., 296(3):769–826, 2010. MR2628822
[25] Fraydoun Rezakhanlou. The coagulating Brownian particles and Smoluchowski’s equation. Markov Process. Related Fields, 12(2):425–445, 2006. MR2249642
[26] Fraydoun Rezakhanlou. Gelation for Marcus-Lushnikov process. Ann. Probab., 41(3B):1806–1830, 2013. MR3098059
[27] L. C. G. Rogers and David Williams. Diffusions, Markov processes, and martingales. Vol. 1. Cambridge Mathematical Library. Cambridge University Press, Cambridge, 2000. Foundations, Reprint of the second (1994) edition. MR1780932
[28] M. Smoluchowski. Drei Vorträge über Diffusion, Brown’sche Molekularbewegung und Koagulation von Kolloidteilchen. Phys. Z. XVII, pages 557–571, 585–599, 1916.
[29] A.-S. Sznitman. Propagation of chaos for a system of annihilating Brownian spheres. Comm. Pure Appl. Math., 40(6):663–690, 1987. MR0910949
[30] Terence Tao. From Bose-Einstein condensates to the nonlinear Schrödinger equation (blog post). http://terrytao.wordpress.com/2009/11/26/from- bose-einstein-condensates-to-the-nonlinear-schrodinger-equation/, 2009.
[31] Cédric Villani. A review of mathematical topics in collisional kinetic theory. In Handbook of mathematical fluid dynamics, Vol. I, pages 71–305. North-Holland, Amsterdam, 2002. MR1942465
[32] Warren H. White. A global existence theorem for Smoluchowski’s coagulation equations. Proc. Amer. Math. Soc., 80(2):273–276, 1980. MR0577758
[33] Dariusz Wrzosek. Mass-conserving solutions to the discrete coagulation-fragmentation model with diffusion. Nonlinear Anal., 49(3, Ser. A: Theory Methods):297–314, 2002. MR1886116
[34] Mohammad Reza Yaghouti, Fraydoun Rezakhanlou, and Alan Hammond. Coagulation, diffusion and the continuous Smoluchowski equation. Stochastic Process. Appl., 119(9):3042–3080, 2009. MR2554038