Асеев В. В.
Квазиконформный аналог критерия Каратеодори мёбиусовости отображенийВ 1937 г. Каратеодори доказал, что инъективное отображение f : G → f (G)
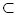
области G
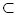
, переводящее окружности в окружности, мёбиусово. В данной статье показано, что если инъективное отображение переводит окружности в k-квазиокружности, то оно K-квазиконформно c K ≤ k +
.
Aseev V. V.
A quasiconformal analog of Carathéodory’s criterion for the Möbius property of mappingsIn 1937, Carathéodory proved that every injective mapping f : G → f (G)
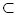
of a domain G
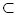
, taking circles to circles, is Möbius. The present article shows that if each injective mapping takes circles onto k-quasicircles then it is K-quasiconformal with K ≤ k +
.
Полный текст статьи / Full texts:
![]()