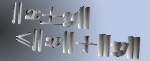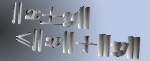| |
|
Abstract: |
An extension of the Bojanic-Stanojevic type inequality [1] is made by considering the 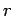 -th derivate of the Dirichlet kernel -th derivate of the Dirichlet kernel 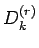 instead of instead of 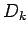 . Namely, the following inequality is proved . Namely, the following inequality is proved
where 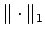 is the is the 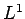 -norm, -norm,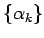 is a sequence of real numbers, is a sequence of real numbers, 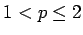 , , 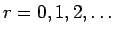 and and 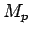 is an absolute constant dependent only on is an absolute constant dependent only on 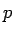 . As an application of this inequality, it is shown that the class . As an application of this inequality, it is shown that the class
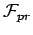 is a subclass of is a subclass of 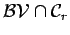 , where , where 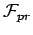 is the extension of the Fomin's class, is the extension of the Fomin's class, 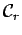 is the extension of the
Garrett-Stanojevic class [8] and is the extension of the
Garrett-Stanojevic class [8] and 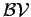 is the class of all null sequences of bounded variation. is the class of all null sequences of bounded variation.
[1] R. BOJANIC and C.V.
STANOJEVIC, A class of L1-convergence, Trans. Amer. Math.
Soc., 269 (1982), 677-683.
[8] Z. TOMOVSKI, An extension of the Garrett- Stanojevic class, Approx. Theory Appl., 16(1) (2000) 46–51. [ONLINE] A corrected version is
available in the RGMIA Research Report Collection, 3(4), Article
3, 2000. URL: http://rgmia.vu.edu.au/v3n4.html
|