| |
|
|
| |
Volume 6, Issue 1, Article 14 |
|
|
|
|
|
| |
An Example of a Stable Functional Equation When the Hyers Method Does Not Work
|
| |
|
Authors: |
Zoltán Kaiser, Zsolt Pales, |
|
| |
|
Keywords:
|
Cauchy's functional equation, Stability, Hyers iteration |
|
| |
|
Date Received:
|
15/12/04 |
|
| |
|
Date Accepted:
|
08/02/05 |
|
| |
|
Subject Codes: |
39B82
|
|
| |
|
Editors: |
John Michael Rassias, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
We show that the functional equation is stable in the classical sense on arbitrary 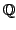 -algebraically open convex sets, but the Hyers method does not work. -algebraically open convex sets, but the Hyers method does not work. For the convenience of the reader, we have included an extensive list of references where stability theorems for functional equations were obtained using the direct method of Hyers.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



