| |
|
|
| |
Volume 6, Issue 4, Article 99 |
|
|
|
|
|
| |
L'Hospital-Type Rules for Monotonicity, and the Lambert and Saccheri Quadrilaterals in Hyperbolic Geometry
|
| |
|
Authors: |
Iosif Pinelis, |
|
| |
|
Keywords:
|
L'Hospital type rules for monotonicity, Hyperbolic geometry, Poincare model, Lambert quadrilaterals, Saccheri quadrilaterals, Riemann geometry, Differential geometry. |
|
| |
|
Date Received:
|
10/08/05 |
|
| |
|
Date Accepted:
|
24/08/05 |
|
| |
|
Subject Codes: |
Primary 53A35, 26A48; Secondary 51M25, 5
|
|
| |
|
Editors: |
Matti Vuorinen, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
Elsewhere we developed rules for the monotonicity pattern of the ratio 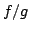 of two functions on an interval of the real line based on the monotonicity pattern of the ratio of two functions on an interval of the real line based on the monotonicity pattern of the ratio 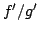 of the derivatives. These rules are applicable even more broadly than the l'Hospital rules for limits, since we do not require that both of the derivatives. These rules are applicable even more broadly than the l'Hospital rules for limits, since we do not require that both 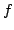 and and 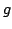 , or either of them, tend to 0 or , or either of them, tend to 0 or  at an endpoint of the interval. at an endpoint of the interval. Here these rules are used to obtain monotonicity patterns of the ratios of the pairwise distances between the vertices of the Lambert and Saccheri quadrilaterals in the Poincaré model of hyperbolic geometry. Some of the results may seem surprising. Apparently, the methods will work for other ratios of distances in hyperbolic geometry and other Riemann geometries. The presentation is mainly self-contained.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|



