| |
|
Abstract: |
Suppose  is a positive homogeneous function defined on is a positive homogeneous function defined on 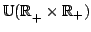 , call , call ![$ H_{f}(a,b;p,q)=left[ frac{{f(a^{p},b^{p})}}{{f(a^{q},b^{q})}}right] ^{frac{1}{p-q}}$](images/155_05_JIPAM/img3.gif) homogeneous function with two parameters. If homogeneous function with two parameters. If  is 2nd differentiable, then the monotonicity in parameters is 2nd differentiable, then the monotonicity in parameters 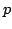 and and  of of 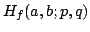 depend on the signs of depend on the signs of  , for variable , for variable 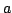 and and 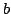 depend on the sign of depend on the sign of ![$ I_{2a}=left[ {(ln f)_{x}ln (y/x)}right] _{y}$](images/155_05_JIPAM/img10.gif) and and ![$ I_{2b}=left[ {(ln f)_{y}ln (x/y)}right] _{x}$](images/155_05_JIPAM/img11.gif) respectively. As applications of these results, a serial of inequalities for arithmetic mean, geometric mean, exponential mean, logarithmic mean, power-Exponential mean and exponential-geometric mean are deduced. respectively. As applications of these results, a serial of inequalities for arithmetic mean, geometric mean, exponential mean, logarithmic mean, power-Exponential mean and exponential-geometric mean are deduced.
|



