| |
|
Abstract: |
Observing that 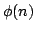 divides divides 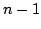 if if 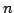 is a prime, where is a prime, where 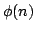 is the well known Euler function, Lehmer has asked whether there is any composite number is the well known Euler function, Lehmer has asked whether there is any composite number 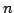 with this property. For this unsolved problem, partial answers were given by several researchers. Considering the unitary analogue with this property. For this unsolved problem, partial answers were given by several researchers. Considering the unitary analogue 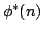 of of 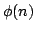 , Subbarao noted that , Subbarao noted that 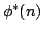 divides divides 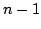 , if , if 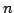 is the power of a prime; and sought for integers is the power of a prime; and sought for integers 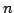 other than prime powers which satisfy this condition. In this paper we improve two inequalities, established by Subbarao and Siva Rama Prasad [5], to be satisfied by other than prime powers which satisfy this condition. In this paper we improve two inequalities, established by Subbarao and Siva Rama Prasad [5], to be satisfied by 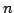 for for 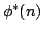 which divides which divides 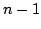 . .
![$ [5]$](images/143_06_JIPAM/img5.gif) M.V. Subbarao and V. Siva Rama Prasad, Some analogues of a Lehmer problem on the totient function, Rocky Mountain Journal of Mathematics; Vol. 15, Number 2: Spring 1985, 609-619. M.V. Subbarao and V. Siva Rama Prasad, Some analogues of a Lehmer problem on the totient function, Rocky Mountain Journal of Mathematics; Vol. 15, Number 2: Spring 1985, 609-619.
|