| |
|
|
| |
Volume 8, Issue 1, Article 25 |
|
|
|
|
|
| |
Approximation of the Dilogarithm Function
|
| |
|
Authors: |
Mehdi Hassani, |
|
| |
|
Keywords:
|
Special function, Dilogarithm function, Digamma function, Polygamma function, Polylogarithm function, Lerch zeta function. |
|
| |
|
Date Received:
|
15/04/06 |
|
| |
|
Date Accepted:
|
03/01/07 |
|
| |
|
Subject Codes: |
33E20.
|
|
| |
|
Editors: |
Alexandru Lupas (1942-2007), |
|
| |
|
|
|
|
|
| |
|
Abstract: |
In this short note, we approximate Dilogarithm function, defined by 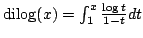 . Letting . Letting we show that for every 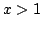 , the inequalities , the inequalities
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|