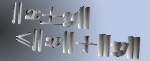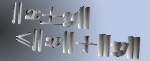| |
|
Abstract: |
The main object of this paper is to introduce and investigate a subclass 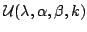 of normalized analytic functions in the open unit disk of normalized analytic functions in the open unit disk 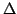 , which generalizes the familiar class of uniformly convex functions. The various properties and characteristics for functions belonging to the class , which generalizes the familiar class of uniformly convex functions. The various properties and characteristics for functions belonging to the class 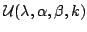 derived here include (for example) a characterization theorem, coefficient inequalities and coefficient estimates, a distortion theorem and a covering theorem, extreme points, and the radii of close-to-convexity, starlikeness and convexity. Relevant connections of the results, which are presented in this paper, with various known results are also considered. derived here include (for example) a characterization theorem, coefficient inequalities and coefficient estimates, a distortion theorem and a covering theorem, extreme points, and the radii of close-to-convexity, starlikeness and convexity. Relevant connections of the results, which are presented in this paper, with various known results are also considered.
|