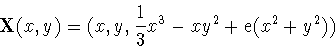
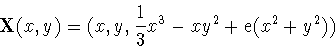
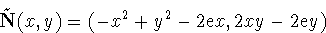
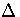 = 4 (x2 + y2 -
= 4 (x2 + y2 -
 2). Since
grad
2). Since
grad 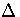 = 4 (2 x, 2 y),
the map Ñ is good if and only if
= 4 (2 x, 2 y),
the map Ñ is good if and only if 
 0. If
0. If
 = 0, then the parabolic set is just the origin. The
modified Gauss mapping then has a two-fold ramification point at the
origin, as can be seen by expressing Ñ in polar
coordinates:
= 0, then the parabolic set is just the origin. The
modified Gauss mapping then has a two-fold ramification point at the
origin, as can be seen by expressing Ñ in polar
coordinates:
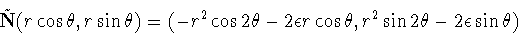
 = 0, we have
= 0, we have
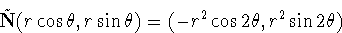
 = 0, the parabolic set is the circle
x2 + y2 =
= 0, the parabolic set is the circle
x2 + y2 =
 2, parametrized by x = |
2, parametrized by x = |
 | cost, y = |
| cost, y = |
 | sin t. The restriction of Ñ to this
circle gives
| sin t. The restriction of Ñ to this
circle gives
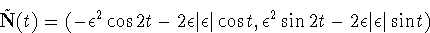
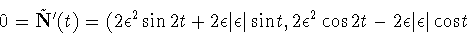
 > 0, this yields the solutions
t = 0, 2
> 0, this yields the solutions
t = 0, 2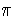 /3, 4
/3, 4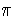 /3, and if
/3, and if  < 0 the
solutions are t =
< 0 the
solutions are t = 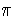 ,
, 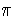 /3, 5
/3, 5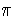 /3. In either case,
it is easy to check that Ñ'(t) = 0
implies Ñ''(t)
/3. In either case,
it is easy to check that Ñ'(t) = 0
implies Ñ''(t)  0. For
0. For

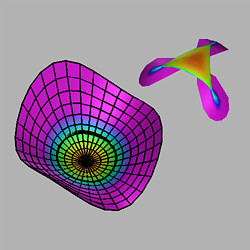
 0, the curve Ñ(t) is a
hypocycloid of three cusps. Thus the Gauss map of the perturbed
monkey saddle is stable for all
0, the curve Ñ(t) is a
hypocycloid of three cusps. Thus the Gauss map of the perturbed
monkey saddle is stable for all 
 0. This unfolding
of the Gauss map of the monkey saddle is identical with the unfolding
of the complex squaring map described by Arnold [A1, pp. 4-5] and
Callahan [C1, pp. 233-234]. (The focal set of the monkey saddle has
an elliptic umbilic singularity at infinity - cf. Section 6 below.)
0. This unfolding
of the Gauss map of the monkey saddle is identical with the unfolding
of the complex squaring map described by Arnold [A1, pp. 4-5] and
Callahan [C1, pp. 233-234]. (The focal set of the monkey saddle has
an elliptic umbilic singularity at infinity - cf. Section 6 below.)
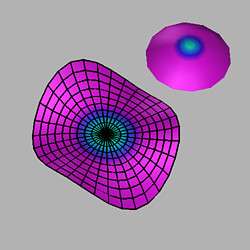
 = 0).
= 0).
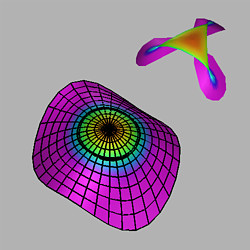
 = -1/2).
= -1/2).
 = 1/2).
= 1/2).
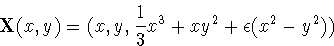
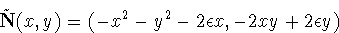
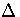 = -4(x2 - y2 -
= -4(x2 - y2 -  2).
Since grad
2).
Since grad 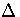 = -4(2x, -2y), the
map N is good if and only if
= -4(2x, -2y), the
map N is good if and only if 
 0. If
0. If
 = 0, the parabolic set is the union of the two lines
y = x and y = -x, and
the modified Gauss mapping is a ``quarter folded handkerchief''
= 0, the parabolic set is the union of the two lines
y = x and y = -x, and
the modified Gauss mapping is a ``quarter folded handkerchief''
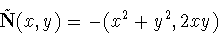
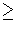 y, x
y, x 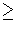 -y},
B = {(x, y) | x
-y},
B = {(x, y) | x 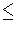 y, x
y, x 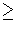 -y},
C = {(x, y) | x
-y},
C = {(x, y) | x 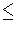 y, x
y, x 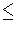 -y},
D = {(x, y) | x
-y},
D = {(x, y) | x 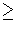 y, x
y, x 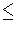 -y} homeomorphically
onto the quadrant C. For
-y} homeomorphically
onto the quadrant C. For 
 0 the parabolic curve is the
hyperbola x2 - y2 =
0 the parabolic curve is the
hyperbola x2 - y2 =  2. To find the cusps of Ñ, we
parametrize the parabolic curve by x = ±
2. To find the cusps of Ñ, we
parametrize the parabolic curve by x = ± cosh t, y =
cosh t, y =  sinh t. The restriction of Ñ to the parabolic curve is then
sinh t. The restriction of Ñ to the parabolic curve is then
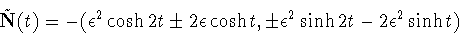
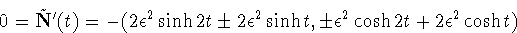

 0 this
yields the unique solution t = 0,
x > 0, and Ñ'(t) = 0 implies
Ñ"(t)
0 this
yields the unique solution t = 0,
x > 0, and Ñ'(t) = 0 implies
Ñ"(t)  0. So the Gauss
map of the handkerchief surface is stable for all
0. So the Gauss
map of the handkerchief surface is stable for all 
 0. This family
of Gauss maps is the same as the unfolding of the quarter folded
handerchief described by Arnold [A1] and
Callahan [18]. (The focal set of the
handkerchief surface for
0. This family
of Gauss maps is the same as the unfolding of the quarter folded
handerchief described by Arnold [A1] and
Callahan [18]. (The focal set of the
handkerchief surface for  = 0 has a
hyperbolic umbilic singularity at infinity.)
= 0 has a
hyperbolic umbilic singularity at infinity.)
 = 0).
= 0).
 = 1/2).
= 1/2).
 = -1/2).
= -1/2).